Persamaan LSTM
Dan dapat berubah-ubah.
Tulisan dibawah ini merupakan ringkasan (dan catatan tambahan pribadi) dari makalah berjudul “Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks” oleh Kratzert, dkk (2018)1.
Informasi Tulisan
| Jenis Tulisan | Catatan Pribadi |
| Unduh (Tulisan Tangan) | OneDrive (PDF) |
| Ilustrasi | Berdasarkan 1 |
DAFTAR ISI
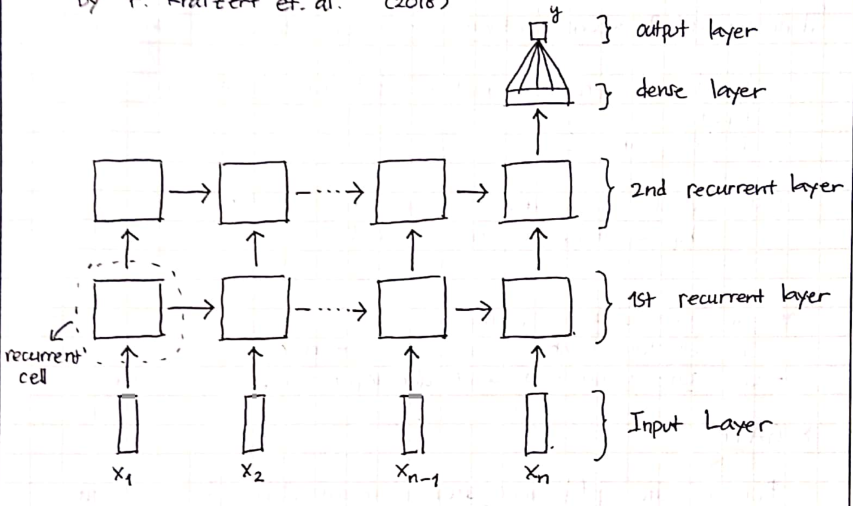
Recurrent Neural Networks (RNN)

Pada sel RNN, hanya terdapat satu internal state $h_t$.
\[\boldsymbol{h}_t = g(\mathbf{W}\boldsymbol{x}_t + \mathbf{U} \boldsymbol{h}_{t-1} + \boldsymbol{b})\]dengan:
- $g(\cdot)$ sebagai activation function, yang digunakan biasanya $\tanh(\cdot)$.
- $\mathbf{W}$ dan $\mathbf{U}$ merupakan matriks bobot dari hidden state dan input $\boldsymbol{x}$.
- $\boldsymbol{b}$ merupakan bias.
catatan:
- $\mathbf{W}, \mathbf{U}, \boldsymbol{b}$ dapat disesuaikan (adjustable).
- $\boldsymbol{h}_t$ diinisiasi dengan nilai $\vec{0}$.
Long Short-Term Memory (LSTM)
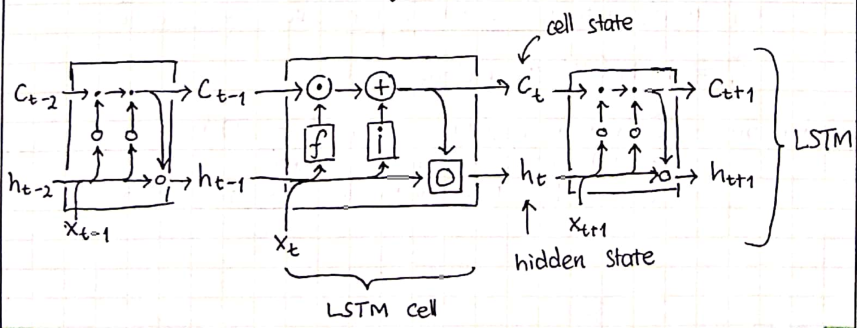
Sebagai perbandingan, LSTM memiliki:
- cell state tambahan atau sel memori $\boldsymbol{c}_t$.
- gate yang mengatur alur informasi pada sel LSTM.
LSTM GATE
Forget Gate ($\boldsymbol{f}$)
Forget gate $\boldsymbol{f}$, mengatur elemen dari vektor cell state $\boldsymbol{c}_{t-1}$ yang akan dilupakan:
\[\boldsymbol{f}_t = \sigma(\mathbf{W}_f\boldsymbol{x}_t+\mathbf{U}_f\boldsymbol{h}_{t-1}+\boldsymbol{b}_f)\]dengan:
- $\sigma(\cdot)$ merupakan persamaan logistik sigmoid.
- $\mathbf{W}_f, \mathbf{U}_f, \boldsymbol{b}_f$ merupakan set parameter yang dapat dilatih di forget gate.
Potential Update Vector ($\widetilde{\boldsymbol{c}}_t$)
Selanjutnya, potential update vector untuk cell state $\widetilde{\boldsymbol{c}}_t$.
\[\widetilde{\boldsymbol{c}}_t=\tanh(\mathbf{W}_{\widetilde{c}}\boldsymbol{x}_t+\mathbf{U}_{\widetilde{c}}\boldsymbol{h}_{t-1}+\boldsymbol{b}_{\widetilde{c}})\]dengan:
- $\widetilde{\boldsymbol{c}}_t$ vektor bernilai rentang $(-1, 1)$.
- $\tanh(\cdot)$ merupakan fungsi hiperbolik tangen.
- $\mathbf{W}_{\widetilde{c}}, \mathbf{U}_{\widetilde{c}}, \boldsymbol{b}_{\widetilde{c}}$ merupakan learnable parameters.
Input Gate ($\boldsymbol{i}$)
Input gate menentukan informasi dari $\widetilde{\boldsymbol{c}}_t$ yang digunakan untuk memperbarui cell state pada current timestep.
\[\boldsymbol{i}_t=\sigma({\mathbf{W}_i\boldsymbol{x}_t+\mathbf{U}_i\boldsymbol{h}_{t-1}+\boldsymbol{b}_i})\]dengan:
- $\boldsymbol{i}_t$, vektor bernilai antara $(0, 1)$.
- $\mathbf{W}_i, \mathbf{U}_i, \boldsymbol{b}_i$: learnable parameters.
Cell State ($\boldsymbol{c}_t$)
Nilai cell state diperbarui dengan:
\[\boldsymbol{c}_t=\boldsymbol{f}_t\odot\boldsymbol{c}_{t-1}+\boldsymbol{i}_t\odot\widetilde{\boldsymbol{c}}_t\]dengan:
- $\boldsymbol{f}_t, \boldsymbol{i}_t$ bernilai pada rentang $(0, 1)$. Variabel tersebut menentukan nilai pada $\boldsymbol{c}_{t-1}, \widetilde{\boldsymbol{c}}_t$ yang perlu diingat $(\boldsymbol{f}_t \approx \vec{1}, \boldsymbol{i}_t\approx\vec{1})$ atau dilupakan $(\boldsymbol{f}_t\approx\vec{0}, \boldsymbol{i}_t\approx\vec{0})$
catatan:
- seperti hidden state, cell state diinisiasi dengan nilai $\vec{0}$.
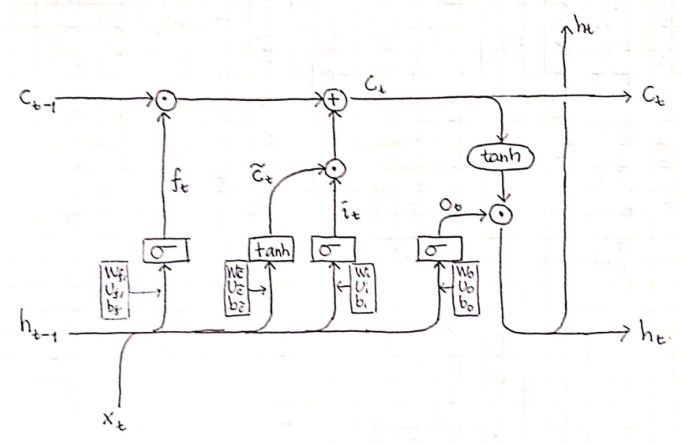
Output Gate ($\boldsymbol{o}$)
Output gate $\boldsymbol{o}$ mengatur informasi dari $\boldsymbol{c}_t$ yang masuk ke hidden state $\boldsymbol{h}_t$.
\[\boldsymbol{o}_t=\sigma(\mathbf{W}_o\boldsymbol{x}_t+\mathbf{U}_o\boldsymbol{h}_{t-1}+\boldsymbol{b}_o)\]dengan:
- $\boldsymbol{o}_t$, vektor bernilai antara $(0, 1)$.
- $\mathbf{W}_o, \mathbf{U}_o, \boldsymbol{b}_o$ merupakan learnable parameters.
Hidden state (LSTM) ($\boldsymbol{h}_t$)
dari $\boldsymbol{o}_t$, diperoleh nilai baru $\boldsymbol{h}_t$:
\[\boldsymbol{h}_t=\tanh(\boldsymbol{c}_t)\cdot\boldsymbol{o}_t\]Final/Output layer ($y$)
pada layer terakhir, nilai hasil sel dihubungkan dengan jaringan/neuron dengan keluaran tunggal.
\[y=\mathbf{W}_d\boldsymbol{h}_n+\boldsymbol{b}_d\]dengan:
- $y$: nilai debit/limpasan.
- $\boldsymbol{h}_n$: hasil dari sel terakhir.
- $\mathbf{W}_d$ sebagai bobot neuron dan $\boldsymbol{b}_d$ sebagai bias.
Ringkasan Persamaan
| No | Persamaan | Fungsi |
|---|---|---|
| 1 | \(\boldsymbol{h}_t = g(\mathbf{W}\boldsymbol{x}_t + \mathbf{U} \boldsymbol{h}_{t-1} + \boldsymbol{b})\) | hidden state (RNN) |
| 2 | \(\boldsymbol{f}_t = \sigma(\mathbf{W}_f\boldsymbol{x}_t+\mathbf{U}_f\boldsymbol{h}_{t-1}+\boldsymbol{b}_f)\) | forget gate |
| 3 | \(\widetilde{\boldsymbol{c}}_t=\tanh(\mathbf{W}_{\widetilde{c}}\boldsymbol{x}_t+\mathbf{U}_{\widetilde{c}}\boldsymbol{h}_{t-1}+\boldsymbol{b}_{\widetilde{c}})\) | potential vector update |
| 4 | \(\boldsymbol{i}_t=\sigma({\mathbf{W}_i\boldsymbol{x}_t+\mathbf{U}_i\boldsymbol{h}_{t-1}+\boldsymbol{b}_i})\) | input gate |
| 5 | \(\boldsymbol{c}_t=\boldsymbol{f}_t\odot\boldsymbol{c}_{t-1}+\boldsymbol{i}_t\odot\widetilde{\boldsymbol{c}}_t\) | cell state |
| 6 | \(\boldsymbol{o}_t=\sigma(\mathbf{W}_o\boldsymbol{x}_t+\mathbf{U}_o\boldsymbol{h}_{t-1}+\boldsymbol{b}_o)\) | output gate |
| 7 | \(\boldsymbol{h}_t=\tanh(\boldsymbol{c}_t)\cdot\boldsymbol{o}_t\) | hidden state (LSTM) |
| 8 | \(y=\mathbf{W}_d\boldsymbol{h}_n+\boldsymbol{b}_d\) | final/dense layer |
Catatan:
- \(\mathbf{x} = \left[\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_n \right]\), merupakan masukan observasi meteorologi dengan complete sequence. Dengan $n$ merupakan jumlah timestep yang digunakan.
- Untuk setiap langkah (timesteps), $\boldsymbol{x}_t$ merupakan vektor berisikan informasi meteorologi pada langkah $t$.
- Pada kasus lapisan LSTM berganda (multiple-stacked LSTM), lapisan berikutnya menerima hasil dari layer sebelumnya, $\mathbf{h}=[\boldsymbol{h}_1, \boldsymbol{h}_2, \cdots, \boldsymbol{h}_n]$.
- Nilai akhir dihitung menggunakan keluaran $\boldsymbol{h}_n$.